Wavelet transform is widely used in image denoising due to its multi-resolution analysis, good ability to characterize signals in the time-frequency domain, and variable-size window. It has a good denoising effect. The wavelet threshold denoising method is one of the most commonly used methods in wavelet denoising in image denoising. The wavelet transform is used to reconstruct the out-of-noise image after wavelet transform. Two important factors in the wavelet threshold denoising method—threshold selection method and threshold function—determine the effect of image denoising directly. Therefore, it is necessary to select the appropriate threshold function and optimal threshold for noise and image to remove the image to the maximum extent. noise.
This paper proposes a new threshold function, which not only satisfies the continuity of the function, but also solves the problem of constant deviation of the threshold function.
1, wavelet threshold denoising principleIn the wavelet threshold denoising method, the noise is usually at a high frequency. With this feature, the high-frequency portion is subjected to corresponding thresholding processing and then reconstructed, thus achieving the purpose of removing noise.
Suppose an image is contaminated with Gaussian noise as follows:

It is a noisy image; nj,k is Gaussian white noise, obeying the normal distribution N(0, δ^2) normal distribution.
The wavelet threshold method is implemented by the following three steps:
1) Wavelet transform is performed on fj,k to obtain wavelet coefficients wj,k;
2) by thresholding the wj, k, the wavelet estimation coefficient w^j, k;
3) Using w^j,k to reconstruct the wavelet coefficients to obtain the denoised image f^j,k.
Commonly used thresholds are: Stein's unbiased likelihood estimation criteria, fixed threshold criteria, heuristic threshold criteria, and minimax principle criteria. This paper uses a fixed threshold criterion to define a fixed threshold as follows:

Where: M&TImes; N is the size of the image.
2, wavelet threshold function 2.1, common wavelet threshold functionAnother name for the wavelet threshold denoising method is the threshold function, that is, the threshold function is used to obtain the threshold. The most widely used threshold function is the threshold method proposed by Donoho et al., and Donoho et al. also prove that the wavelet threshold is used to denoise the ratio. The classic denoising method is superior. Then on this basis, people proposed improved threshold functions, such as hard and soft compromise threshold functions. The hard and soft threshold functions are as shown in equation (3)(4).
The hard threshold function is defined as:

Hard and soft threshold methods have achieved good results in denoising, but they have disadvantages. Although equation (3) solves the error problem of |w^j,k-wj,k|, there is a discontinuity of ±λ, which will generate some additional oscillations during image reconstruction, and it is more prone to visual distortion such as Pseudo-Gibbs phenomenon. . Similarly, equation (4) has good continuity at ±λ, but there is a constant error in |w^j,k-wj,k|, which causes distortion of the high-frequency information of the image, and the equation (4) There is a difficulty in high-order derivation, which is not conducive to further processing it with mathematical tools. The hard and soft compromise threshold function improves the equation (3)(4), but there is still a constant deviation problem.
In order to better solve the problems caused by the above methods, the literature proposes the following improved threshold functions:
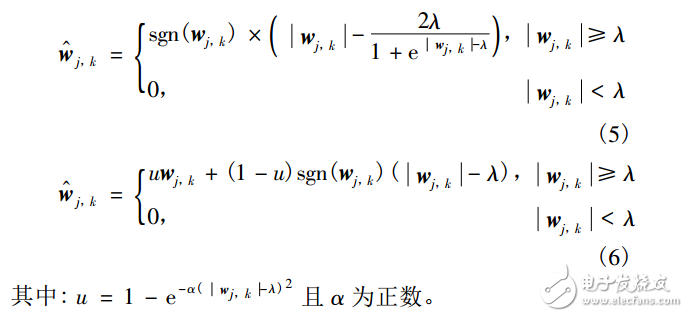
Equation (5) solves the error problem of the wavelet coefficients of the noisy image and the constant wavelet coefficient, but it has no adjustment factor, which is obviously not flexible enough, and the continuity is poor. Although equation (6) solves the continuity problem, However, the constant deviation of the wavelet coefficients of the noisy image from the estimated wavelet coefficients has not been well solved. In order to effectively solve the above problems, this paper proposes a new function:
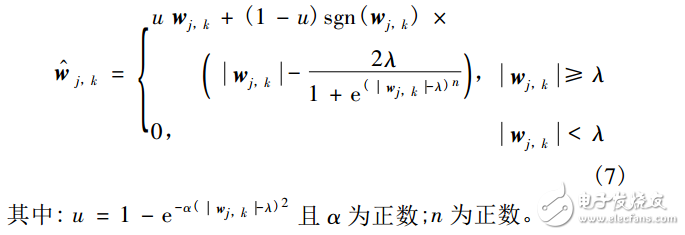
The abscissa of Fig. 1 is the original wavelet coefficient obtained by wavelet transform of fj, k; the ordinate is the estimated wavelet coefficient obtained by threshold processing the wavelet coefficients. λ is the threshold value; drawing is performed according to the function of equation (7). In Fig. 1, λ=5, the original wavelet coefficient ranges from -20 to 20.
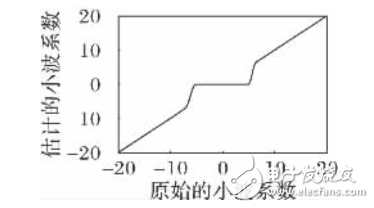
Figure 1 α=1, n=3 improved threshold function
Shenzhen ChengRong Technology Co.,Ltd. , https://www.dglaptopstandsupplier.com