1. Mean
The mean value represents the magnitude of the DC component in the signal, represented by E(x). For Gaussian white noise signal, its mean value is 0, so it has only AC component.
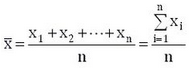
2. The square of the mean
The square of the mean value is represented by {E(x)}^2, which represents the power of the DC component in the signal.
3. Mean square value
The mean square value represents the mean value after the signal is squared, and is represented by E(x^2). The mean square value represents the average power of the signal. Signal average power = signal AC component power signal DC component power
For example: find the mean square value of x, y, z. Mean square value = (x squared y squared z squared)/3
4. Root mean square value
Root mean square value, use RMS (root mean square), which is the root of the mean square value
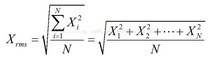
5. Mean square error
Mean square error (mean square error), expressed in MSE. The mean square error is the average of the sum of squares of the distances of each data from the true value, that is, the average of the sum of squares of errors. The calculation formula is close to the variance in form. Its root is called the root mean square error, and the root mean square error is only the standard deviation Close in form. Mean square error is sometimes considered equivalent to variance
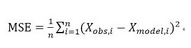
6. Root mean square error
The root mean square error is represented by RMSE (root mean square error). It is the square root of the ratio of the square of the deviation between the observation value and the true value to the number of observations n. In actual measurement, the number of observations n is always limited, and the true value can only be replaced by the most reliable (optimal) value. Root error It is very sensitive to the very large or very small errors in a group of measurements, so the root mean square error can well reflect the precision of the measurement. The root mean square error is sometimes referred to as the standard deviation

7. Variance
Variance is expressed by variance or deviation or Var. Variance describes the fluctuation range of the signal, indicating the strength of the AC component in the signal, that is, the average power of the AC signal.
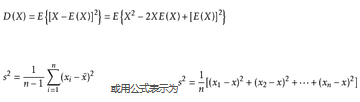
Note that the above division is n-1, only then the variance estimated from the sample value is unbiased, that is, the expectation of the above formula is the variance of X. However, in some places, it is also useful to divide by n to express the variance, but the result obtained in this way is not an unbiased estimate of the variance, and the mathematical expectation of the calculation result is not the variance of X, but a multiple of the variance of X.
8. Standard deviation
The standard deviation (Standard Deviation) is expressed by σ, and sometimes the standard deviation can be called the root mean square error RMSE. The standard deviation is the average of the distance of each data from the mean. It is the square root of the square and average of the deviation from the mean. It is represented by σ. The standard deviation can reflect the degree of dispersion of a data set.
The standard deviation σ reflects the degree to which the measured data deviates from the true value. The smaller the σ, the higher the measurement accuracy, so σ can be used as the standard for evaluating the accuracy of this measurement process.
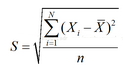
Why use standard deviation with variance? What are the advantages of standard deviation over variance?
Because the variance is inconsistent with the dimension of the data we want to process, although it can describe the degree of deviation of the data from the mean, the processing result does not conform to our intuitive thinking.
For example: there are 60 students in a class, the average grade is 70 points, the standard deviation is 9, the variance is 81, and the grades follow a normal distribution. Then we cannot intuitively determine how many points the class students deviate from the mean through the variance. , Through the standard deviation, we can intuitively get that the probability that the student's scores are distributed in the range of [61,79] is 0.6826, which is approximately equal to 34.2%*2 in the figure below.
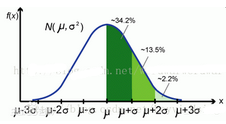
to sum up:
(1) In general, mean square error, root mean square error and variance, standard deviation are not equal, although their formulas are similar. We need to distinguish between the true value and the mean value
(2) For variance and standard deviation, they reflect the relationship between the data series and the mean.
(3) For the mean square error and root mean square error, they reflect the relationship between the data series and the true value.
AE Bar,AE Bar Vape,Original factory AE,China AE Vape
Nanning Nuoxin Technology Co., LTD , https://www.nx-vapes.com